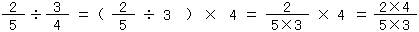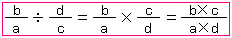トップページに戻る
けいさんゲーム算数5・6年
小数・分数のまとめ

算数5・6年けいさんゲームは、楽しみながら、計算がはやく、正しくできるようになる学習ゲームです。
この「てびき」をよく読んでから、けいさんゲームを始めましょう。
<もくじ>
<計算に強くなろう!>
(1)計算ゲームなのです。
このゲームは、楽しいゲームだけではありません。楽しい中に、計算がはやく、正しくできるようになるための工夫がされています。ですから、けいさんゲームを何回もするうちに、知らず知らずのうちに計算の力がついてきます。
(2)あせらずに、じっくりとやろう。
計算に強くなるコツ…それは、毎日少しずつコツコツと計算問題をやることです。問題をたくさんやれば、それだけ計算がはやく、正しくできるようになります。つまり、計算に強くなる近道なんてないのです。
(3)計算で考えてほしいこと。
計算がはやく、正しくできるようになるのと同時に、計算の意味やしかたの理由を知ることも、とても大切です。そのために、計算で考えてほしいことがいくつかあります。それらが『この計算で考えてほしいこと』にまとめてあります。
(4)計算をやくだてよう。
『この計算で考えてほしいこと』をよく読んで、ゲームで計算の力を身につけたら、じっさいに使うことが大切です。お買いものをした時とか、工作をする時など、いろいろな生活の場面で使ってみるのです。そして、もっと便利で、かんたんなしかたはないかな、ほかの場合はどうかなと、ちょっと考えてみましょう。
<けいさんゲームの内容>
このカセットでは、2つのゲームで、下の各コースの計算にチャレンジできます。
キミが使っている教科書と見くらべて、じょうずにけいさんゲームをしてください。
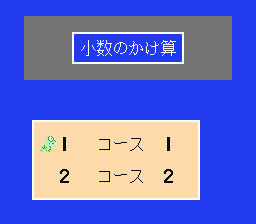
(1)小数のかけ算(5年) 《スペースファイター》
| コース1 |
整数×小数の計算 |
| コース2 |
小数×小数の計算 |
(2)小数のわり算(5年) 《スペースファイター》
| コース1 |
小数÷小数の計算(あまりのない場合) |
| コース2 |
小数÷小数の計算(あまりのある場合) |
(3)分数のたし算とひき算(5年) 《よっちゃんのお花畑》
| ①分数のたし算 |
コース1 |
真分数+真分数の計算(異分母) |
| コース2 |
帯分数をふくむ分数のたし算(異分母) |
| ②分数のひき算 |
コース1 |
真分数-真分数の計算(異分母) |
| コース2 |
帯分数をふくむ分数のひき算(異分母) |
(4)分数のかけ算とわり算(5・6年) 《よっちゃんのお花畑》
| ①分数のかけ算 |
コース1(5年) |
真分数×整数の計算 |
| コース2(5年) |
帯分数×整数の計算 |
| コース3(6年) |
真分数(整数をふくむ)×真分数の計算 |
| コース4(6年) |
帯分数(真分数をふくむ)×帯分数の計算 |
| ②分数のわり算 |
コース1(5年) |
真分数÷整数の計算 |
| コース2(5年) |
帯分数÷整数の計算 |
| コース3(6年) |
真分数(整数をふくむ)÷真分数の計算 |
| コース4(6年) |
帯分数(真分数をふくむ)÷帯分数の計算 |
<コントローラーの説明>
1人でゲームをする時は、Ⅰコントローラーを使います。
2人でゲームをする時は、ⅠコントローラーとⅡコントローラーの両方を使います。
<さあ、はじめよう>
(1)ゲームを遊ぼう。
上の画面の中から、やりたいゲームを選ぼう。
| ① |
十字ボタンの上・下キーかSELECTボタンで、やりたいゲームの所に合わせる。 |
| ② |
STARTボタンをおす。 |
(2)コースを選ぼう。
上記『けいさんゲームの内容』のコースの内容を見て、コースを選ぼう。
| ① |
十字ボタンの上・下キーかSELECTボタンで、どちらかに合わせる |
| ② |
STARTボタンをおす。 |
(3)ゲームをする人数を選ぼう。
けいさんゲームは、1人でも2人でも楽しむことができます。
| ① |
十字ボタンの上・下キーかSELECTボタンで、どちらかに合わせる |
| ② |
STARTボタンをおす。 |
さあ、これで準備は終わりです。
| 注意 |
| ● |
選びかたをまちがえた時は、AまたはBボタンをおしましょう。最初の画面にもどるので、もういちどはじめから、選んでください。 |
|
(4)ゲームスタート!
| ● |
2人でゲームをする時
ⅠコントローラーとⅡコントローラーの両方を使います。2人のとく点で、ゲームをしているほうの文字がフラッシュします。答えをまちがえたりして、フラッシュする文字がかわったら、相手の人に交代しましょう。 |
| ● |
とちゅうでゲームを中断したい時
STARTボタンをおしてください。もう一度おすと、続きが始まります。 |
| ● |
とちゅうでゲームを終わりたい時
SELECTボタンとSTARTボタンをいっしょにおしてください。最初の画面にもどります。 |
(5)ゲームが終わったら……
| ● |
Aボタン
もう一度、同じゲームが始まります。 |
| ● |
Bボタン
最初の画面にもどります。 |
<【1】スペースファイター>
「スペースファイター」は、戦とう機をあやつって敵の基地を攻撃していくスリリングなゲームだ。この基地には、各所に人間の脳がうめこんであるんだ。そこが基地の指令部になっている。君の任務は、この基地の指令部を完全に破壊することにある。たよりは、君の計算力と反射神経だけである。
さあ、宇宙に向かってテイク・オフ!
●ゲームのやりかた
ゲームは大きく2つの場面に分かれる。場面1から説明しよう。
主人公は、宇宙せんとう機T-56。君はT-56をじょうずにあやつって、敵の宇宙ステーションをさがし出し、破壊していくんだ。基地の中では、さまざまな種類の戦とう機が攻撃してくるので、それをかわしながら攻撃して進んで行こう。
 |
| ▲ T-56 |
宇宙ステーションの入口近くまで来ると、T-56は操縦不能になって、敵の宇宙ステーションの中に、すいこまれていく。ここで場面2に切り変わるよ。
 |
| ▲ 入口 |
場面2では、いよいよ君の計算力が必要になってくる。画面右側には問題が表示されている。また、画面左側には0~9までの数字が書かれた、爆弾の信管が並んでいる。そして、問題の横には、この信管をはめこむ穴があいている。
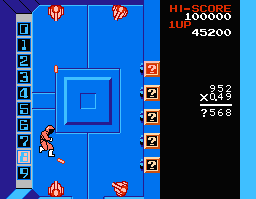 |
| ▲ 場面2 |
主人公は、T-56から降りた少年アース。君は、少年アースを動かして、問題式の"?"にあてはまる数字が書かれた信管を、穴に運んでいくんだ。ただし、まちがった数字が書かれた信管を選んだら、アウトだぞ。また、四方から敵のビーム攻撃があるから、気をつけよう。
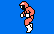 |
| ▲ 少年アース |
さて、"?"に全部正しい答えが入ったら、少年アースはその宇宙ステーションを破壊したことを意味する。下の出口から出て、再びT-56に乗って、場面1の基地の中を進んで行こう。そして、次の宇宙ステーションをさがし出し、破壊するんだ。
このようにして基地の中をすすんでいくと、やがて人間の脳をうめこんだ、指令部があらわれてくる。指令部からは、はげしい攻撃があるぞ。君は、それをかわしながら、この指令部をおおっているバリアーめがけて、どんどん砲弾をうちこもう。指令部を完全に破壊したら、ステージ1は終了だ。次のステージに進もう。
 |
| ▲ 指令部 |
●コントローラーの使いかた
戦とう機T-56と少年アースは、カーソルキー十字ボタンを使って動かそう。
T-56から砲弾を発射させたい時は、Aボタンをおそう。
答えは、左側の数字が書かれた信管をAボタンで選び、問題の左側にある信管をはめこむ穴に、Aボタンでセットしよう。
問題を解き終わるごとに、T-56から発射される砲弾のスピードのレベルを、Bボタンで切り変えることができるぞ。
でも、1度死ぬと、レベル1にもどるよ。
●小数点のうちかた
小数のかけ算の時は、数字を入れ終わったら、十字ボタンで小数点をセットしよう。
小数のわり算の時は、まず、わる数とわられる数の小数点を十字ボタンで移動しよう。
コース2では、最後にあまりの小数点を十字ボタンでセットしよう。
<【2】よっちゃんのお花畑>
「よっちゃんのお花畑」は、パズル的な要素がもりこまれている高度な頭脳ゲームだ。もちろん、君の計算力も必要だよ。
さあ、よっちゃんといっしょに頭の体操をしよう!
●ゲームのやりかた
ゲームのルールはいたって簡単。主人公の女の子"よっちゃん"をじょうずに動かして、問題式の点めつしている"?"にあてはまるバスケットの中に、黄色の果実を入れるんだ。でもまちがった数字のバスケットに入れたり、赤色の果実を入れたりすると、残りタイムが減ってしまうぞ。
 |
| ▲ よっちゃん |
|
ルールは簡単だけど、果実を動かすにはちょっとしたテクニックが必要だ。それを説明しよう。
黄色い果実も赤い果実も最初は種の状態で、それから芽が出て、花が咲き、果実になる。そして果実になるまでは動かせないんだ。でもじょうろで水をかけてあげると、早く成長させることができるよ。
よっちゃんの力で運べる果実は、一度に1つだけ。2つ以上をいっぺんに運ぶことはできない。また、運ぶ方向に種や芽、花があっても動かすことができないので、気をつけよう。
もうひとつやっかいなのは、お花畑の中によっちゃんの行く手をはばむ、じゃまものがいることだ。じゃまものは下の2種類。
 |
 |
| ▲ 大カマドウマ |
▲ ヘッドスネーク |
彼らにつかまったら、おしまいだ。でも、彼らにも弱点がある。スプレーをかけられると、少しの間だけ動けなくなるんだ。その間は、よっちゃんはつかまる心配がないよ。じゃまものの上を通り抜けることだってできるんだ。ただし、スプレーは使いすぎると、だんだん効果がうすくなるよ。
また、大カマドウマもヘッドスネークも、種や芽、花、果実のあるところは通り抜けることができない。だから、果実を動かして、彼らを閉じこめて身動きできないようにするという手もあるぞ。
●コントローラーの使いかた
よっちゃんはカーソルキー十字ボタンを使って移動させよう。
スプレーは、かけたい方向に向けてAボタンをおそう。
じょうろで水をまく時も、同じようにして、Bボタンをおそう。
●アイテム
 |
スプレー
スプレーを使いすぎても、このアイテムがあれば、もとの効果にもどるよ。 |
 |
オーバー・ザー・シード
種の上を、果実が動かせるようになるんだ。 |
 |
チェンジ
赤色の花に水をかけると、黄色の花にかわるよ。 |
| このほかにもかくれアイテムがいくつかあるよ。果実を動かした時にアイテムに変わったら、確実に手に入れて、有効に使おう。
|
<【1】小数のかけ算>
(1)4×3はどうして12なの?
決まってるじゃないか、4のかたまりが3つ分で、四三12だ。
そうだね。4×3は、1かたまり4このものが3つ分という意味だね。
(2)それじゃ、4×3.2はどういう意味?
4×3.2だって、1かたまり4このものが3.2……あれ? 3.2つ分?っておかしいね。3つ分より少し多いってことかな?
そう、3.2つ分っておかしいね。算数では、このことを3.2倍というんだったね。
(3)「3.2倍すること」の意味
3つ分より少し多いというのはとてもいいね。そこをもう少しはっきりさせよう。
3.2倍するというのを、数直線をつかって、次のようにきめたらどうだろう。
『3.2倍すること、つまり4×3.2は、4を1とみて、3.2にあたるところを求める計算』としたらどうだろう。
そうすると、4×0.6は、4を1とみて0.6にあたるところ(▼)を求める計算となる。
(4)かけられる数より小さくなる。
▼のように、1より小さい数をかけると、かけられる数(この場合4)より小さくなることもあるんだ。いままでかけたら大きくなるという頭はもう古いことになるね。
<【2】小数のわり算>
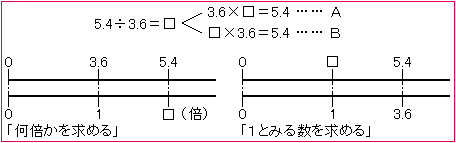
(1)わり算の2つの意味、覚えている?
3年生のときに、わり算には2つの使い方があったのを覚えているかい?
そうそう、Aタイプのかける数を求めるときと、Bタイプのかけられる数を求めるときだね。たとえば、Aタイプは「何人分?」、Bタイプは「1人分は?」という問題だったね。
(2)「小数でわる」ときは?
ところが、2.4人分とか、0.8人分というふうに、小数でわるときや、商が小数ででてきたときに、おかしくなっちゃうね。
(3)わり算の意味
そこで、かけ算と同じように、わり算も次のように決めたらどうだろう。
かけ算の意味をもとに考えると、Aタイプは「何倍を求めるとき」、Bタイプは「1とみる数を求めるとき」の計算がわり算となる。
(4)わると大きくなるときもある。
そうすると、5.4÷0.8のように、1より小さい数でわると、わられる数より大きくなるときもあるんだね。
<【3】分数のたし算とひき算>
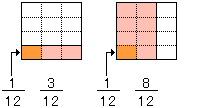
(1)分母の異なる分数のたし算のしかた
4年生で分数のたし算は、分母が同じ分数だったね。ところが、今度はたとえば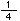 +
+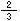 のような分母が異なるたし算なんだ。
のような分母が異なるたし算なんだ。
どうすればいいのかな?
そうそう、分母をそろえれば(通分)よいわけだね。
(2)なぜ分母をそろえるの?
それでは、なぜ通分して分母をそろえるのかな? なぜ分母がそろったら、たすことができるのかな?
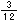 は
は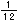 が3つ、
が3つ、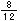 は
は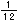 が8つあつまったものだね。つまり、もとにする
が8つあつまったものだね。つまり、もとにする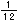 (
( )が同じだから、たすことができるんだね。算数では、このもとにする大きさのことを、単位というんだ。
)が同じだから、たすことができるんだね。算数では、このもとにする大きさのことを、単位というんだ。
つまり、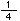 は
は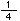 の単位が1つ、
の単位が1つ、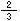 は
は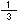 の単位が2つということで、単位がちがうからたせないんだ。
の単位が2つということで、単位がちがうからたせないんだ。
整数のたし算や小数のたし算でも、位をそろえるよね。あれも、単位をそろえてたしていることになるんだ。共通した考えがそこにあるんだね。
(1)通分がポイント
分数のひき算も、分母をそろえて(通分)からひき算をするね。どうして分母をそろえるかというと、同じ単位にしないとひけないからだね。
ただ、注意したいのは、通分するときは、できるだけ小さい数をみつけるようにしようね。
<【4】分数のかけ算とわり算 (5年)>
(1)分数に整数をかける計算のしかた
たとえば、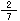 ×3を例にして考えてみよう。
×3を例にして考えてみよう。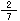 は、そうそう
は、そうそう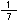 という単位が2つという意味だよね。その3倍ということだから、その単位
という単位が2つという意味だよね。その3倍ということだから、その単位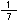 が2×3こあることだね。
が2×3こあることだね。
計算のしかたをまとめると、つぎのようになるよ。
(2)帯分数のときどうする?
それでは、帯分数のときはどうしたらいいだろうね。例えば、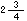 ×2というときはどうするのだろうね。
×2というときはどうするのだろうね。
そうそう、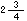 を
を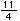 となおせば、(1)のしかたがつかえるね。つまり、帯分数は、そう! 仮分数になおしてかけるんだね。
となおせば、(1)のしかたがつかえるね。つまり、帯分数は、そう! 仮分数になおしてかけるんだね。
(3)とちゅうの約分
上の例で、かけた答えを約分しているね。かけたあとで約分することも大切だけれど、とちゅうで約分してもいいんだよ。
とちゅうで約分すると、計算がはやいね。
(1)分数を整数でわる計算のしかた
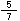 ÷3の計算を考えよう。
÷3の計算を考えよう。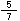 ÷3は、
÷3は、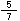 を3等分して、1とみるものを求めることだから、下の図のようになるね。
を3等分して、1とみるものを求めることだから、下の図のようになるね。
分数の単位をさらにこまかくすることになるんだ。7等分してあるものを、さらに3等分するわけだから、7×3等分するわけだね。つまり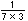 が5つで
が5つで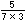 となる。これを式に表すと、
となる。これを式に表すと、
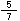 ÷3以外の例で考えても、いつも分数の単位をこまかくするわけだから、下のようにまとめることができるね。
÷3以外の例で考えても、いつも分数の単位をこまかくするわけだから、下のようにまとめることができるね。
(2)帯分数のときはどうする?
もうわかるよね。そう、かけ算のときと同じように、仮分数になおせばいいね。
そうそう、とちゅうで約分できるときは、約分しておくと、計算がかんたんになるのだったね。
<【4】分数のかけ算とわり算 (6年)>
(1)分数に分数をかける計算のしかた
分数に分数をかける計算のしかたを考えてみよう。ちょっとむずかしそうだね。
1mが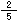 kgで、
kgで、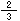 mにあたるところを求めるのだから、
mにあたるところを求めるのだから、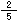 ×
×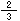 と式がたつね。1とみるところがわかっていて、その
と式がたつね。1とみるところがわかっていて、その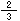 倍を求めるのだからね。
倍を求めるのだからね。
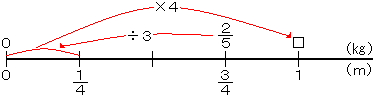
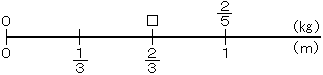
上の直線をよくみよう。□のところを求めればいいんだ。どうしたらいいかな。
まず、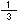 mでは何kgかを考えればいいんだ。なぜなら、それを2倍すれば、
mでは何kgかを考えればいいんだ。なぜなら、それを2倍すれば、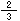 mの重さがでるからだよ。
mの重さがでるからだよ。
つまり、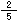 kgを3でわると▽のところがでて、それに2をかけると□がでるね。
kgを3でわると▽のところがでて、それに2をかけると□がでるね。
それを式で表すと、
分数×分数の計算のしかたをまとめると、
となるわけだ。
つまり、分母は分母どうし、分子は分子どうしかけるといいわけだね。
(1)分数を分数でわる計算のしかた
分数を分数でわる計算のしかたを考えよう。
1とみるところを求める計算だから、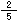 ÷
÷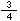 という式がたつね。上の数直線を手がかりに、□のところを求めるしかたを考えてみよう。
という式がたつね。上の数直線を手がかりに、□のところを求めるしかたを考えてみよう。
まず、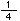 mでは何kgか考えればよいわけだ。なぜなら、それを4倍すれば、1とみる□のところをだすことができるからだね。
mでは何kgか考えればよいわけだ。なぜなら、それを4倍すれば、1とみる□のところをだすことができるからだね。
それを式に表すと、次のようになるね。
分数÷分数の計算のしかたをまとめると、次のようになる。
つまり、分数でわる計算は、わる数の分母と分子を入れかえて(逆数といいます)かけることになるわけだね。
帯分数のときは仮分数になおしたり、とちゅうで約分できるときは約分することも忘れないでね。

トップページに戻る
















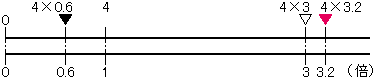

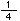 +
+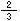 のような分母が異なるたし算なんだ。
のような分母が異なるたし算なんだ。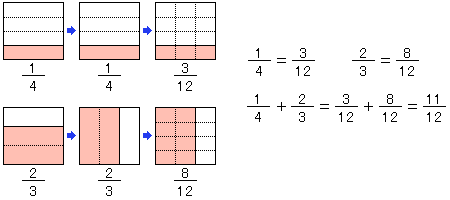
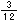 は
は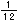 が3つ、
が3つ、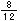 は
は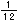 が8つあつまったものだね。つまり、もとにする
が8つあつまったものだね。つまり、もとにする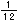 (
( )が同じだから、たすことができるんだね。算数では、このもとにする大きさのことを、単位というんだ。
)が同じだから、たすことができるんだね。算数では、このもとにする大きさのことを、単位というんだ。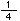 は
は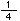 の単位が1つ、
の単位が1つ、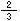 は
は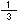 の単位が2つということで、単位がちがうからたせないんだ。
の単位が2つということで、単位がちがうからたせないんだ。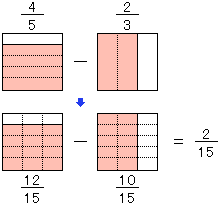
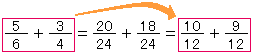
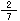 ×3を例にして考えてみよう。
×3を例にして考えてみよう。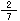 は、そうそう
は、そうそう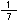 という単位が2つという意味だよね。その3倍ということだから、その単位
という単位が2つという意味だよね。その3倍ということだから、その単位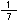 が2×3こあることだね。
が2×3こあることだね。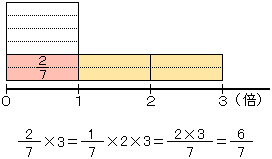
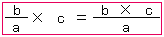
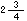 ×2というときはどうするのだろうね。
×2というときはどうするのだろうね。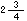 を
を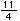 となおせば、(1)のしかたがつかえるね。つまり、帯分数は、そう! 仮分数になおしてかけるんだね。
となおせば、(1)のしかたがつかえるね。つまり、帯分数は、そう! 仮分数になおしてかけるんだね。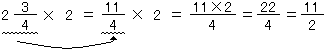
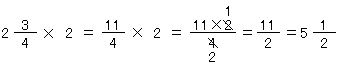
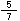 ÷3の計算を考えよう。
÷3の計算を考えよう。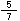 ÷3は、
÷3は、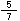 を3等分して、1とみるものを求めることだから、下の図のようになるね。
を3等分して、1とみるものを求めることだから、下の図のようになるね。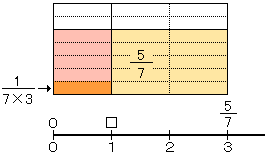
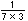 が5つで
が5つで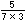 となる。これを式に表すと、
となる。これを式に表すと、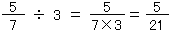
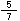 ÷3以外の例で考えても、いつも分数の単位をこまかくするわけだから、下のようにまとめることができるね。
÷3以外の例で考えても、いつも分数の単位をこまかくするわけだから、下のようにまとめることができるね。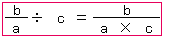
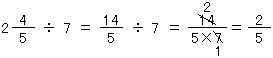
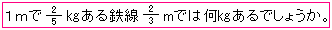
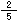 kgで、
kgで、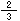 mにあたるところを求めるのだから、
mにあたるところを求めるのだから、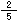 ×
×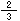 と式がたつね。1とみるところがわかっていて、その
と式がたつね。1とみるところがわかっていて、その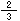 倍を求めるのだからね。
倍を求めるのだからね。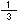 mでは何kgかを考えればいいんだ。なぜなら、それを2倍すれば、
mでは何kgかを考えればいいんだ。なぜなら、それを2倍すれば、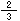 mの重さがでるからだよ。
mの重さがでるからだよ。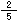 kgを3でわると▽のところがでて、それに2をかけると□がでるね。
kgを3でわると▽のところがでて、それに2をかけると□がでるね。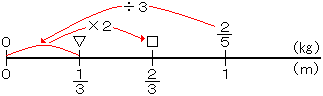
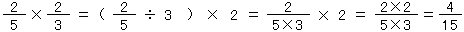


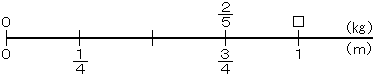
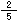 ÷
÷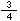 という式がたつね。上の数直線を手がかりに、□のところを求めるしかたを考えてみよう。
という式がたつね。上の数直線を手がかりに、□のところを求めるしかたを考えてみよう。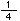 mでは何kgか考えればよいわけだ。なぜなら、それを4倍すれば、1とみる□のところをだすことができるからだね。
mでは何kgか考えればよいわけだ。なぜなら、それを4倍すれば、1とみる□のところをだすことができるからだね。